Trigonometri Hesaplamaları

Trigonometri, üçgenlerin kenarları ve açıları arasındaki ilişkileri inceleyen bir matematik dalıdır.

Her düz kenarlı şekil bir üçgen koleksiyonu olarak bölünebileceğinden, trigonometri tüm geometride bulunur. Dahası trigonometri, özellikle karmaşık sayılar, sonsuz seriler, logaritmalar ve kalkülüs gibi matematiğin diğer dallarıyla şaşırtıcı derecede karmaşık ilişkilere sahiptir.

Trigonometri (Yunanca trigönon "üçgen" + metron "ölçmek" ), üçgenlerin açıları ile kenarları arasındaki bağıntıları konu edinen matematik dalı. Trigonometri sayesinde üçgendeki kenar ve açıların (3 kenar ve 3 açı, toplam 6 değer) bir tanesi kenar olmak şartıyla en az üç tanesini bildiğimizde diğerlerini hesaplayabiliriz.

Trigonometrik Hesaplama, trigonometrik fonksiyonlar denilen, açı ve kenar bağıntılarından oluşturulmuş formüller yardımıyla yapılır. Bu fonksiyonlar temel fonksiyonlar olan Sinüs (Sine / Sinus), Kosinüs (Cosine / Cosinus) ve Tanjant (Tangent) ve bu fonksiyonlardan türetilmiş Sekant (Secant), Kosekant (Cosecant) ve Cotanjant (Cotangent) fonksiyonlarıdır.

Trigonometri, mühendislik ve sanatta matematiğin en yoğun kullanılan dalıdır.

Trigonometri konusu içinde üçgen olan her yerde işe yarar. İlk zamanlarda yıldızların konumunu ölçmek ve arazi ölçümleri yapmak gibi işler için kulanılan trigonometri zaman içinde bilim ve teknolojinin her alanında kullanılır olmuştur.

Matematiğin geometri gibi bir çok alanında ve fizik biliminde trigonometriden fazlaca yararlanılır.

Örneğin yapılarda eğer dik üçgen şeklinde bir bölüm varsa, yüksekliğe ve genişliğe göre bu üçgen birimin taban açısının ne olması gerektiği trigonometri yardımıyla hesaplanıp çıkan sonuca göre kalıp yapma, kiriş veya kolon koyma, kullanılacak malzemenin boyutları veya hangi malzemelerin sipariş edileceği gibi kararlar alınabilir. Yine yapılarda daire şeklinde bölümler varsa bu dairenin parçaları ile igili Hesaplama da trigonometri kullanılarak yapılır.

Bilgisayar alanında da trigonometriden oldukça fazla yararlanılmaktadır. Artık bir çok makine parçası tasarımı veya yapı tasarımı gibi işlemler bilgisayarlar aracılığıyla yapıldığından, bu ve benzeri işlemleri yapan bilgisayar programları yaptıkları Hesaplamada tasarlanan parçadaki uzunluk ve açıları ölçmek için yoğun olarak trigonometriden faydalanırlar.

Bilgisayarla ilgili bir başka örnek bilgisayar oyunları için verilebilir. Bir bilgisayar oyununda yukarıya doğru açılı olarak fırlatılan bir topun (balon patlatma veya yastık oyunu gibi) fırlatma aracının açısına göre yön alması ve açıya uygun bir çizgide gidebilmesi için trigonometri kullanılarak Hesaplama yapılır.

Trigonometrik fonksiyonlar, üçgenin kenarlarının birbirine oranlarını ifade eden Sinüs (Sine / Sinus), Kosinüs (Cosine / Cosinus) ve Tanjant (Tangent) ve bu fonksiyonlardan türetilmiş Sekant (Secant), Kosekant (Cosecant) ve Cotanjant (Cotangent)'dır (Trigonometri işlemleri yaparken bunların tümünün oran olduğunu aklımızdan çıkarmamalıyız).

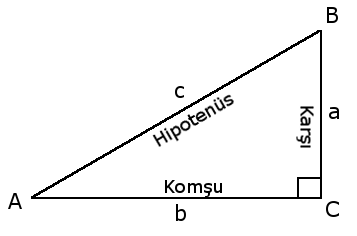
Modern matematikte kullanılan trigonometrik oranlar şunlardır

(A açı değeri olmak üzere)

Sinüs A = a / c = Karşı Kenar / Hipotenüs
(Sinüs A, A açısının sinüsü demektir.)

Kosinüs A = b / c = Komşu Kenar / Hipotenüs

Tanjant A = a / b = Karşı Kenar / Komşu Kenar

Kosekant A = c / a = Hipotenüs / Karşı Kenar

Sekant A = c / b = Hipotenüs / Komşu Kenar

Kotanjant A = b / a = Komşu Kenar / Karşı Kenar

Kosekant fonksiyon aynı zamanda sinüs fonksiyonunun çarpmaya göre tersidir. Yani;
1 / Sinüs A aynı sonucu verecektir. Dolayısıyla;

Kosekant A = 1 / Sinüs A

da diyebiliriz.

Sekant fonksiyonu ise kosinüs fonksiyonunun çarpmaya göre tersidir. Dolayısıyla;

Sekant A = 1 / Kosinüs A

şeklinde de hesaplanabilir.

Kotanjant fonksiyonu da tanjant fonksiyonunun çarpmaya göre tersidir. Dolayısıyla;

Kotanjant A = 1 / Tanjant A

aynı sonucu verir.