Trigonometrik Bağıntılar (Eşitlikler / Özdeşlikler / Identities)

Matematikte bağıntı, aynı sonucu veren (ve doğal olarak birbirine eşit olan ve birbirini doğrulayan) bir eşitliğin iki tarafında gösterilen matematiksel ifadelerdir.

Bağıntı kelimesinden eşitliğin her iki tarafının birbirine bağlı olmasını (birinin sonucunun diğerinin sonucunu da vermesini) ve bunun hiç bir zaman değişmediğini anlayabilirsiniz.

Trigonometrik bağıntılar ise bir dik üçgenle ilgili bağıntılardır (Dik üçgen olmayan üçgenlerle ilgili bağıntılar bu sayfanın konusu değildir).

En temel trigonometrik bağıntılardan ve aynı zamanda kotanjantı gösteren bağıntıyı örnek verelim. A, açı olmak üzere.

cot(A) = 1 / tan(A)

Yani bir açının kotanjant değeri, 1 sayısının açının tanjant değerine bölümüne eşittir. Yani tanjant ve kotanjant birbirlerinin çarpmaya göre tersidir.

Tabi buradan;

tan(A) = 1 / cot(A)

sonucunu da çıkarabiliriz ki bu da bir bağıntıdır.

Kotanjant fonksiyonunun aynı zamanda komşu kenarın karşı kenara oranını temsil ettiğini de hesaba katarsak bağıntıyı,

cot(A) = 1 / tan(A) = Komşu Kenar / Karşı Kenar

şeklinde uzatabiliriz. Alttaki birim çemberden görüleceği üzere birim çemberde karşı kenarın uzunluğu açının sinüsü, komşu kenarın uzunluğu ise açının kosinüsü olduğuna göre (Birim çemberin yarıçapı 1 olduğundan, içerde gösterilen üçgenin hipotenüs uzunluğu 1'dir. Bundan dolayı açının sinüsü ile karşı komşu kenarın uzunluğu, kosinüsü ile de komşu kenarın uzunluğu aynı olur.);

aynı bağıntıyı

cot(A) = 1 / tan(A) = cos(A) / sin(A)

şeklinde de yazabiliriz. Görüldüğü gibi trigonometrik fonksiyonlar (sinüs, kosinüs, tanjant, ...) birbirine bağlıdırlar (değerleri birbirine bağlı olarak değişmektedir).

Birim Çemberde Bağıntılar (Örnek)

Alttaki birim çember gösteriminde pembe daireyi sürükleyerek açıyı değiştirin ve açıya göre üstteki bağıntıda yer alan ifadelerin değerlerini ve birim çemberin yanında gösterilen sonuçlarını inceleyin. Görüleceği gibi açı değiştikçe değerler ve eşitliklerin sonuçları birbirine bağlı olarak değişmektedir (bağıntıda verilen tüm ifadelerin sonucu aynıdır yani incelediğimiz bağıntıya göre açının kotanjantına eşittir).

Bağıntılar trigonometride ve matematiğin diğer alanlarında büyük kolaylıklar sağlar. Bağıntıları bilmek matematikte işimizi çok kolaylaştırır. Bazı problemleri daha kolay çözmemizi sağlarlar.

Bağıntıda bulunan eşitliklerden biri ile karşılaştığımızda bunun diğer eşitlikle aynı sonucunu verdiğini bildiğimizden doğrudan diğer eşitlikteki değerleri bulabilir veya çözümümüzü diğer eşitliği kullanarak devam ettirebiliriz.

Örneğin üstte verdiğimiz bağıntıyı biliyorsak, karşımıza açının sinüs ve kosinüs değerlerinin verildiği bir soru çıktığında kosinüs değerini sinüs değerine böldüğümüzde kotanjant değerini bulabilir ve soruya göre buna göre cevap verebilir veya çözümü kotanjant değeri üzerinden devam ettirebiliriz.

Bağıntıları akılda tutmak zordur. Bu nedenle bağıntıları öğrenirken birim çemberde bağıntıyı görmek ve incelemek yararlıdır.

Tanımlayıcı Bağıntılar / Eşitlikler

Bunlar, sinüs ve kosinüs kullarak tanjant, kotanjant, sekant ve kosekantı tanımlarlar (hesaplamamızı sağlarlar). Dikkat! Bu bağıntıları mutlaka bilmeliyiz.

tan θ = sin θ / cos θ
cot θ = 1 / tan θ = cos θ / sin θ
sec θ = 1 / cos θ
csc θ = 1 / sin θ

Ayrıca sinüs ile kosekant, kosinüs ile sekant ve tanjant ile kotanjant birbirlerinin çarpmaya göre tersi olduğundan alttaki eşitliklerin de bilinmesi gerekir.

sin θ = 1 / csc θ
csc θ = 1 / sin θ

cos θ = 1 / sec θ
sec θ = 1 / cos θ

tan θ = 1 / cot θ
cot θ = 1 / tan θ

Sinüs ve Kosinüs İçin Pisagor Bağıntısı

Bir çok kaynakta belirtildiği üzere muhtemelen en önemli bağıntı budur.

sin² θ = cos² θ = 1

Tabi buradan alttaki eşitlikleri de elde ederiz.

tan² θ + 1 = sec² θ
1 + cot² θ = csc² θ

Kare ifadeleri açının değil, örneğin sin² θ için, hesaplanacak sinüs değerinin karesi anlamındadır.

Tümleyen Açı Bağıntıları

sin θ = cos(90° - θ)
cos θ = sin(90° - θ)
tan θ = cot(90° - θ)
cot θ = tan(90° - θ)
sec θ = csc(90° - θ)
csc θ = sec(90° - θ)

Açılar (ifadelerdeki θ) radyan olarak verildiğinde eşitlikler aşağıdaki gibi yazılır (360 derece 2π radyandır. Dolayısıyla π radyan (yani yaklaşık 3,14 radyan) 180 dereceye, π / 2 radyan ise 90 dereceye karşılık gelir).

sin θ = cos(π / 2 - θ)
cos θ = sin(π / 2 - θ)
tan θ = cot(π / 2 - θ)
cot θ = tan(π / 2 - θ)
sec θ = csc(π / 2 - θ)
csc θ = sec(π / 2 - θ)

Trigonometrik Fonksiyonların Periyodikliği (Periyodik / belirli aralıklarla tekrar eden olması)

Birim çember sayfamızdaki grafikten de görülebileceği gibi grafikte herhangi bir fonksiyonu gösteren dalganın (sinüs, kosinüs, ...) tepe noktaları arasındaki bölüme 1 periyot denir ve 360 derecede bir tekrar eder.

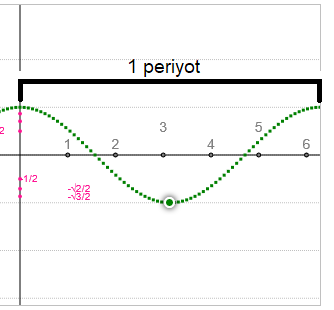
Sinüs, kosinüs, sekant ve kosekant için, açının fonksiyon değeri, açının 360 (2π radyan) dereceye eklenmesi ile bulunan açının fonksiyon değeri ile aynıdır. 360 dereceden çıkarılması ile bulunan açının fonksiyon değeri ise değerin negatif halidir.

Örneğin;
30 derecenin sinüs değeri 0,5'dir. 360 + 30 = 390 derecenin sinüs değeri de 0,5'dir.
-30 derecenin sinüs değeri -0,5'dir. 360 - 30 = 330 derecenin sinüs değeri de -0,5'dir.

Tanjant ve kotanjant için ise bir periyot 180 derecedir (π radyan).

sin (θ + 360) = sin θ
cos (θ + 360) = cos θ
sec (θ + 360) = sec θ
csc (θ + 360) = csc θ

tan (θ + 180) = tan θ
cot (θ + 180) = tan θ

Negatif Açılar İçin Bağıntılar

sin(-θ) = -sin(θ)
cos(-θ) = cos(θ)
tan(-θ) = -tan(θ)

Üstte bağıntılar için örnek:

sin(-45) = -0,7071... = -(sin(45)) = -(0,7071...)

Bağıntılar bu kadar değildir. Daha bir çok bağıntı vardır ve türetilebilir. İhtiyaç halinde bu bağıntıları da öğrenmeniz gerekebilir. Ancak yukarıda da bahsettiğimiz gibi bağıntıları akılda tutmak zordur. Bunun için mutlaka Trigonometrik Eşitlikleri Öğrenmek İçin Kolay Bir Yol sayfamızı inceleyiniz.