Kosekant Hesaplama

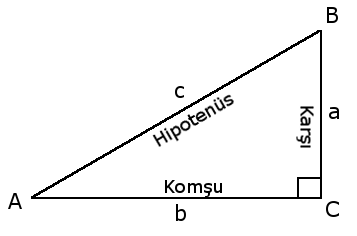
Dik üçgende bir açının kosekantı, hipotenüs isimli kenarın, açının karşısındaki dik kenara oranıdır. Kosekant aynı zamanda, aynı açının sinüsünün çarpmaya göre tersidir (1'in sinüs değerine bölümüdür). Şekle göre hipotenüsün (c kenarı) a kenarına oranı, A açısının kosekantını verir. Kosekant, kısaca Csc şeklinde ifade edilir. Bulunan bu değere A açısının kosekantı denir ve Csc(A) şeklinde gösterilir.

Kosekant
$$\sec (A)=\frac{\mathrm{Hipotenüs}}{\mathrm{Karşı\; Kenar}}=\frac{c}{a}=\frac{1}{\sin (A)}$$
şeklinde ifade edilir.

Hipotenüsün karşı kenara bölünmesiyle bulunan değer, ilgili açıya karşılık gelen bir orandır (A açısının Kosekant değeridir). Tüm trigonometrik oranlar gibi açı sabit, uzunluklar değişirse oran aynı kalır.

Birim Çemberde Kosekant Gösterimi

Ark Kosekant (veya ters Kosekant), bir Kosekant değerinin karşılık geldiği açıyı gösteren fonksiyondur. Arccosecant, acsc veya csc^-1 şeklinde gösterilir. Örneğin: asin(x), sin^-1(x)

(Uyarı: csc^-1 ifadesindeki -1 bir üs değildir. Fonksiyonun tersini belirtmek için kullanılmaktardır.)

Ark kosekant ve diğer ters trigonometrik fonksiyonlar ile ilgili daha geniş bilgiyi Ters Trigonometrik Fonksiyonlar sayfamızda bulabilir ve ark kosekant hesaplayabilirsiniz.